بزرگترین مقسوم علیه مشترک و کوچکترین مضرب مشترک یکی از مفاهیم پایه در ریاضیات است. برخلاف ظاهر ساده آنها کاربردهای بسیاری در زمینههای مختلفی دارند. برای محاسبه این دو عدد راههای ریاضیاتی متفاوتی وجود دارد. در بین این راهها برخی از آنها برای کدنویسی در محیط متلب مناسبتر هستند. در این پست پس از بررسی دو تا از راههای بیشتر متداول، نحوه محاسبه این مقادیر در متلب را با هم مرور میکنیم.
آموزش رسم نمودار سه بعدی در میپل
بزرگترین مقسوم علیه مشترک
بزرگترین مقسوم علیه مشترک بین دو عدد عددی است که هر دوی آن اعداد بر آن عدد بخشپذیر باشند. یا به عبارت دیگر باقیمانده تقسیم آن اعداد بر بزرگترین مقسوم علیه مشترکشان صفر است. یکی از راههای بدستآوردن آن استفاده از اعداد اول است. هر عددی را میتوان به فاکتورهای اولش تجزیه کرد. اعداد اول اعدادی هستند که فقط به 1 و خودشان بخشپذیر هستند (مانند 2، 3، 5، و غیره). برای بدست آوردن بزرگ ترین مقسوم علیه مشترک با استفاده از اعداد اول بصورت زیر باید عمل کرد:
آموزش تصویری رسم نمودار اینتراکتیو یا تعاملی در میپل
بزرگترین مقسوم علیه مشترک به روش فاکتورهای اول:
ابتدا هر کدام از اعداد را به فاکتورهای اولش تجزیه میکنیم.
سپس بزرگترین مقسوم علیه مشترک بین آنها (به عنوان مثال 18 و 48) را بصورت زیر محاسبه میکنیم:
فاکتورهای اول عدد 18:
18=2*3*3
فاکتورهای اول عدد 48:
48=2*2*2*2*3
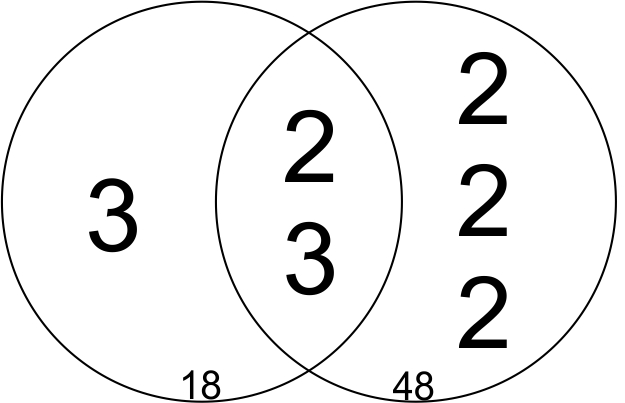
بزرگترین مقسوم علیه مشترک بین آنها عبارتند از:
Greatest common divisor: 2*3=6
و کوچکترین مضرب مشترک بین آنها عبارتند از:
Least common multiple: 3*(2*3)*2*2*2=144
بزرگترین مقسوم علیه مشترک به روش اقلیدس:
در این روش ابتدا عدد بزرگتر را به عدد کوچکتر تقسیم میکنیم. سپس باقیمانده تقسیم را محاسبه میکنیم.
در صورتی که باقیمانده تقسیم صفر شد عدد کوچکتر همان بزرگترین مقسوم علیه مشترک است.
در غیر اینصورت عدد کوچکتر را به باقیمانده تقسیم میکنیم.
باقیمانده تقسیم جدید را حساب میکنیم.
در صورتی که صفر باشد عدد کوچکتر در تقسیم جواب است.
در غیر اینصورت عدد کوچکتر را به باقیمانده تقسیم میکنیم.
به همین ترتیب تا جایی ادامه میدهیم که باقیمانده تقسیم صفر شود. هر گاه باقیمانده صفر شد عدد کوچکتر در آن تقسیم بزرگ ترین مقسوم علیه مشترک بین دو عدد دلخواه است. به عنوان مثال برای دو عدد 48 و 18 بصورت زیر عمل میکنیم.
48/18 -> 12 — 18/12 -> 6 — 12/6 ->0
بنابراین در تقسیم آخر که باقیمانده صفر شد عدد کوچکتر یعنی 6 بزرگترین مقسوم علیه مشترک بین 48 و 18 است.
در پایان هم برای بدست آوردن کوچکترین مضرب مشترک حاصلضرب دو عدد را بر بزرگ ترین مقسوم علیه مشترک تقسیم میکنیم.
18*48/6=144
تبدیل پایان نامه (تز) به مقاله ISI
بزرگترین مقسوم علیه مشترک در متلب
حال برای پیاده سازی عملیات بالا (روش اقلیدس) در متلب بصورت زیر عمل میکنیم:
بعد از دریافت اعداد موردنظر توسط دستور input باید آنها را از بزرگتر به کوچکتر مرتب کرد. برای این کار از یک دستور if استفاده میکنیم.
سپس باقیمانده تقسیم عدد بزرگتر به عدد کوچکتر را با استفاده از دستور mod محاسبه میکنیم. اگر باقیمانده صفر شد عدد کوچکتر پاسخ مساله است.
در غیر اینصورت با استفاده از یک حلقه while مراحل ریاضی گفتهشده در بالا را تا آنجایی ادامه میدهیم که باقیمانده تقسیم عدد بزرگتر بر عدد کوچکتر برابر صفر گردد.
در پایان با تقسیم حاصلضرب اعداد اولیه بر بزرگترین مقسوم علیه مشترک کوچکترین مضرب مشترک را بدست میآوریم.
سپس با استفاده از دستور disp مقادیر محاسبه شده را نمایش میدهیم.
دانلود رایگان کد متلب برای بزرگترین مقسوم علیه مشترک به روش اقلیدس

سلام علیکم
بزرگترین مقسوم علیه بین سه عدد؟
سلام وقت بخیر
دو راه برای یافتن برزگترین مقسوم علیه مشترک بین سه عدد وجود دارد. راه اول این است که ابتدا بین دو عدد ب.م.م را پیدا کنید و سپس ب.م.م نهایی را بین عدد سوم و ب.م.م مرحله قبل محاسبه کنید. راه دیگر این است که فاکتورهای عدد اول مشترک بین همه آنها را در نظر بگیرید که این روش (برای دو عدد) در همین پست توضیح داده شده است.
سورس کد ب.م.م و ک.م.م(مقسوم علیههای مشترک) سه عدد در متلب::
n=input(‘n= ‘);
m=input(‘m=’ );
k=input(‘k= ‘);
p=n*m;
if m
temp=m;
m=n;
n=temp;
end
while n>0
r=rem(m,n);
m=n;
n=r;
end;
m1=m;
cm1=p/m;
k1=k;
if m
temp=m;
m=k;
k=temp;
end;
while k>0
r=rem(m,k);
m=k;
k=r;
end;
disp(‘max’);
disp(m);
m=cm1;
n=k1;
p=n*m;
if m
temp=m;
m=n;
n=temp;
end;
while n>0
r=rem(m,n);
m=n;
n=r;
end;
cm=p/m;
disp(‘cm(a,b,c)=’);
disp(cm);